ESTADÍSTICA
La Estadística es la ciencia cuyo objetivo es reunir una
información cuantitativa concerniente a individuos, grupos, series de hechos,
etc. y deducir de ello gracias al análisis de estos datos unos significados
precisos o unas previsiones para el futuro.
La estadística, en general, es la ciencia que trata de la
recopilación, organización presentación, análisis e interpretación de datos
numéricos con e fin de realizar una toma de decisión más efectiva.
TIPOS DE GRAFICAS PARA REPRESENTAR DATOS ESTADISTICOS
Los gráficos son medios popularizados y a menudo los más
convenientes para presentar datos, se emplean para tener una representación
visual de la totalidad de la información. Los gráficos estadísticos
presentan los datos en forma de dibujo de tal modo que se pueda percibir
fácilmente los hechos esenciales y compararlos con otros.
Tipos de gráficos estadísticos
·
Barras
·
Líneas
·
Circulares
·
Áreas
·
Cartogramas
·
Mixtos
·
Histogramas
Otros
·
Dispersograma
·
Pictogramas
Gráficos de barras verticales
Representan valores usando trazos verticales, aislados o no unos
de otros, según la variable a graficar sea discreta o continua.
Gráficos de barras horizontales
Representan valores discretos a base de trazos horizontales,
aislados unos de otros. Se utilizan cuando los textos correspondientes a cada
categoría son muy extensos.
Gráficos de barras proporcionales
Se usan cuando lo que se busca es resaltar la representación de
los porcentajes de los datos que componen un total.
Gráficos de barras comparativas
Se utilizan para comparar dos o más series, para comparar
valores entre categorías.
Gráficos de barras apiladas
Se usan para mostrar las relaciones entre dos o más
series con el total.
Gráficos de líneas
En este tipo de gráfico se representan los valores de los datos en
dos ejes cartesianos ortogonales entre sí.
Estos gráficos se utilizan para representar valores con grandes
incrementos entre sí.
Gráficos circulares
Estos gráficos nos permiten ver la distribución interna de los
datos que representan un hecho, en forma de porcentajes sobre un total. Se
suele separar el sector correspondiente al mayor o menor valor, según lo que se
desee destacar.
Gráficos de Áreas
En estos tipos de gráficos se busca mostrar la tendencia de la información
generalmente en un período de tiempo.
Cartogramas
Estos tipos de gráficos se utilizan para mostrar datos sobre una
base geográfica. La densidad de datos se puede marcar por círculos, sombreado,
rayado o color.
Gráficos Mixtos
En estos tipos de gráficos se representan dos o más series de
datos, cada una con un tipo diferente de gráfico. Son gráficos más vistosos y
se usan para resaltar las diferencias entre las series.
Histogramas
Estos tipos de gráficos se utilizan para representa distribuciones
de frecuencias. Algún software específico para estadística grafican la curva de
gauss superpuesta con el histograma.
OTROS Gráficos
En esta categoría se encuentran la mayoría de los gráficos
utilizados en publicidad. Se los complementa con un dibujo que esté relacionado
con el origen de la información a mostrar. Son gráficos llamativos, atraen
la atención del lector.
Dispersograma
Los dispersogramas
Son gráficos que se construyen sobre dos ejes ortogonales de
coordenadas, llamados cartesianos, cada punto corresponde a un par de
valores de datos x e y de un mismo elemento suceso.
Pictogramas
Los pictogramas son gráficos similares a los gráficos de barras,
pero empleando un dibujo en una determinada escala para expresar la unidad de
medida de los datos. Generalmente este dibujo debe cortarse para representar
los datos.
Es común ver gráficos de barras donde las barras se reemplazan por
dibujos a diferentes escalas con el único fin de hacer más vistoso el gráfico,
estos tipos de gráficos no constituyen un pictograma.
MEDIDAS DE TENDENCIA CENTRAL
Media, Mediana, Moda
Las medidas de tendencia central (media, mediana y moda) sirven
como puntos de referencia para interpretar las calificaciones que se obtienen
en una prueba.
Volviendo a nuestro ejemplo, digamos
que la calificación promedio en la prueba que hizo el alumno fue de 20
puntos. Con este dato podemos decir que la calificación del alumno se ubica
notablemente sobre el promedio. Pero si la calificación promedio fue de 65
puntos, entonces la conclusión sería muy diferente, debido a que se ubicaría
muy por debajo del promedio de la clase.
En resumen, el propósito de las medidas
de tendencia central es:
Mostrar en qué lugar se ubica la
persona promedio o típica del grupo.
Sirve como un método para comparar o
interpretar cualquier puntaje en relación con el puntaje central o típico.
Sirve como un método para comparar el
puntaje obtenido por una misma persona en dos diferentes ocasiones.
Sirve como un método para comparar los
resultados medios obtenidos por dos o más grupos.
Las medidas de tendencia central más
comunes son:
La media aritmética: comúnmente conocida como media o promedio. Se representa por
medio de una letra M o
por una X con una
línea en la parte superior.
La mediana: la cual es el puntaje que se ubica en el centro de una
distribución. Se representa como Md.
La moda: que es el puntaje que se presenta con mayor frecuencia en
una distribución. Se representa Mo.
De estas tres medidas de tendencia
central, la media es
reconocida como la mejor y más útil. Sin embargo, cuando en una distribución se
presentan casos cuyos puntajes son muy bajos o muy altos respecto al resto del
grupo, es recomendable utilizar la mediana o la moda. (Porque dadas las
características de la media, esta es afectada por los valores extremos).
La media es considerada como la mejor
medida de tendencia central, por las siguientes razones:
Los puntajes contribuyen de manera
proporcional al hacer el cómputo de la media.
Es la medida de tendencia central más
conocida y utilizada.
Las medias de dos o más distribuciones
pueden ser fácilmente promediadas mientras que las medianas y las modas de las
distribuciones no se promedian.
La media se utiliza en procesos y
técnicas estadísticas más complejas mientras que la mediana y la moda en muy
pocos casos.
Cómo
calcular, la media, la moda y la mediana
Media
aritmética (X) o promedio
Es aquella medida que se obtiene
al dividir la suma de todos los
valores de una variable por la frecuencia total. En palabras más
simples, corresponde a la suma de un conjunto de datos dividida por el número
total de dichos datos.
Ejemplo 1:
En matemáticas, un alumno tiene las
siguientes notas: 4, 7, 7,
2, 5, 3
n = 6 (número total de datos)
La media aritmética de las notas de esa asignatura es 4,8. Este
número representa el promedio.
Ejemplo 2:
Cuando se tienen muchos datos es más
conveniente agruparlos en una tabla de frecuencias y luego calcular la media
aritmética. El siguiente cuadro con las medidas de 63 varas de pino lo ilustra.
Largo (en
m)
|
Frecuencia
absoluta
|
Largo por
Frecuencia absoluta
|
5
|
10
|
5
. 10 = 50
|
6
|
15
|
6
. 15 = 90
|
7
|
20
|
7
. 20 = 140
|
8
|
12
|
8
.
12 = 96
|
9
|
6
|
9
. 6 = 54
|
Frecuencia
total = 63
|
430
|
Se debe recordar que la frecuencia absoluta indica
cuántas veces se repite cada valor, por lo tanto, la tabla es una manera más
corta de anotar los datos (si la frecuencia absoluta es 10, significa que el
valor a que corresponde se repite 10 veces).
Moda (Mo)
Es la medida que indica cual dato tiene
la mayor frecuencia en
un conjunto de datos; o sea, cual se repite más.
Ejemplo 1:
Determinar la moda en el siguiente
conjunto de datos que corresponden a las edades de niñas de un Jardín Infantil.
5, 7, 3, 3, 7, 8, 3, 5, 9, 5, 3, 4, 3
La edad que más se repite es 3, por lo
tanto, la Moda es 3 (Mo = 3)
Ejemplo 2:
20, 12, 14, 23, 78,
56, 96
En este conjunto de datos no existe ningún valor que se
repita, por lo tanto, este conjunto de valores no tiene moda.
Mediana (Med)
Para reconocer la mediana, es necesario
tener ordenados los valores sea de mayor a menor o lo contrario. Usted divide
el total de casos (N) entre dos, y el valor resultante corresponde al número
del caso que representa la mediana de la distribución.
Es el valor central de un conjunto de valores ordenados en forma creciente o
decreciente. Dicho en otras palabras, la Mediana corresponde al valor que deja
igual número de valores antes y después de él en un conjunto de datos
agrupados.
Según el número de valores que se
tengan se pueden presentar dos casos:
Si el número de valores es impar, la
Mediana corresponderá al valor
central de dicho conjunto de datos.
Si el número de valores es par, la
Mediana corresponderá al promedio de los dos valores centrales (los valores
centrales se suman y se dividen por 2).
Ejemplo 1:
Se tienen los siguientes datos:
5, 4, 8, 10, 9, 1, 2
Al ordenarlos en forma creciente, es
decir de menor a mayor, se tiene: 1, 2, 4, 5, 8, 9, 10
El 5 corresponde a la Med, porque es el
valor central en este conjunto de datos impares.
Ejemplo 2:
El siguiente conjunto de datos está
ordenado en forma decreciente, de mayor a menor, y corresponde a un conjunto de
valores pares, por lo tanto, la Med será el promedio de los valores centrales.
21, 19, 18,
15, 13, 11, 10, 9, 5, 3
Ejemplo 3:
Interpretando el gráfico de barras
podemos deducir que:
5 alumnos obtienen puntaje de 62
5 alumnos obtienen puntaje de 67
8 alumnos obtienen puntaje de 72
12 alumnos obtienen puntaje de 77
16 alumnos obtienen puntaje de 82
4 alumnos obtienen puntaje de 87
lo que hace un total de 50 alumnos
Sabemos que la mediana se obtiene
haciendo
lo cual significa que la mediana
se ubica en la posición intermedia entre los alumnos 25 y 26 (cuyo promedio es
25,5), lo cual vemos en el siguiente cuadro:
puntaje
|
alumnos
|
62
|
1
|
62
|
2
|
62
|
3
|
62
|
4
|
62
|
5
|
67
|
6
|
67
|
7
|
67
|
8
|
67
|
9
|
67
|
10
|
72
|
11
|
72
|
12
|
72
|
13
|
72
|
14
|
72
|
15
|
72
|
16
|
72
|
17
|
72
|
18
|
77
|
19
|
77
|
20
|
77
|
21
|
77
|
22
|
77
|
23
|
77
|
24
|
77
|
25
|
77
|
26
|
77
|
27
|
77
|
28
|
77
|
29
|
77
|
30
|
82
|
31
|
82
|
32
|
82
|
33
|
82
|
34
|
82
|
35
|
82
|
36
|
82
|
37
|
82
|
38
|
82
|
39
|
82
|
40
|
82
|
41
|
82
|
42
|
82
|
43
|
82
|
44
|
82
|
45
|
82
|
46
|
87
|
47
|
87
|
48
|
87
|
49
|
87
|
50
|
El alumno 25 obtuvo puntaje de 77
El alumno 26 obtuvo puntaje de 77
Entonces, como el total de alumnos es
par debemos promediar esos puntajes:
La mediana es 77, lo cual significa que
25 alumnos obtuvieron puntaje desde 77 hacia abajo (alumnos 25 hasta el 1 en el
cuadro) y 25 alumnos obtuvieron puntaje de 77 hacia arriba (alumnos 26
hasta el 50 en el cuadro).
Ver: PSU:
Estadística y Probabilidades;
Fuente
Internet:
MEDIDAS DE DISPERSION
Las medidas de dispersión nos informan sobre cuánto se alejan del
centro los valores de la distribución.
Las medidas de dispersión son:
Rango o recorrido
El rango es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Desviación media
La desviación respecto a la media es la diferencia entre cada valor de la variable estadística y la media
aritmética.
Di = x - x
La desviación media es la media
aritmética de los valores
absolutos de las desviaciones respecto a la media.
La desviación media se representa por
Ejemplo Calcular la desviación media de
la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Desviación media para datos agrupados
Si los datos vienen agrupados en una tabla
de frecuencias, la expresión de la desviación
media es:
Ejemplo Calcular la desviación media de
la distribución:
xi
|
fi
|
xi · fi
|
|x - x|
|
|x - x| · fi
|
|
[10, 15)
|
12.5
|
3
|
37.5
|
9.286
|
27.858
|
[15, 20)
|
17.5
|
5
|
87.5
|
4.286
|
21.43
|
[20, 25)
|
22.5
|
7
|
157.5
|
0.714
|
4.998
|
[25, 30)
|
27.5
|
4
|
110
|
5.714
|
22.856
|
[30, 35)
|
32.5
|
2
|
65
|
10.174
|
21.428
|
21
|
457.5
|
98.57
|
Varianza
La varianza es la media
aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
La varianza se representa por:
Varianza para datos agrupados
Para simplificar el cálculo de la varianza vamos o utilizar las siguientes
expresiones que son equivalentes a las anteriores.
Varianza para datos agrupados
Ejercicios de varianza Calcular la varianza de
la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Calcular la varianza de la distribución de la tabla:
xi
|
fi
|
xi · fi
|
xi2 · fi
|
|
[10, 20)
|
15
|
1
|
15
|
225
|
[20, 30)
|
25
|
8
|
200
|
5000
|
[30,40)
|
35
|
10
|
350
|
12 250
|
[40, 50)
|
45
|
9
|
405
|
18 225
|
[50, 60
|
55
|
8
|
440
|
24 200
|
[60,70)
|
65
|
4
|
260
|
16 900
|
[70, 80)
|
75
|
2
|
150
|
11 250
|
42
|
1 820
|
88 050
|
Propiedades de la varianza
1. La varianza será siempre un valor
positivo o cero, en el caso de que las puntuaciones sean
iguales.
2. Si a todos los valores de la variable se les suma un número la varianza no varía.
3. Si todos los valores de la variable se multiplican por un número la varianza queda multiplicada por elcuadrado de dicho número.
4. Si tenemos varias distribuciones con la
misma media y conocemos sus respectivas varianzas se puede calcular lavarianza total.
Observaciones sobre la varianza
1. La varianza, al
igual que la media, es un índice muy sensible a las puntuaciones extremas.
2. En los casos que no se pueda hallar la media tampoco será posible hallar la varianza.
3. La varianza no viene expresada en las mismas
unidades que los datos, ya que las desviaciones están elevadas al cuadrado.
Desviación típica
La desviación típica es la raíz
cuadrada de la varianza.
Es decir, la raíz cuadrada de la media
de los cuadrados de las puntuaciones de desviación.
La desviación típica se representa por σ.
Calcular la desviación típica de la distribución de la tabla:
xi
|
fi
|
xi · fi
|
xi2 · fi
|
|
[10, 20)
|
15
|
1
|
15
|
225
|
[20, 30)
|
25
|
8
|
200
|
5000
|
[30,40)
|
35
|
10
|
350
|
12 250
|
[40, 50)
|
45
|
9
|
405
|
18 225
|
[50, 60)
|
55
|
8
|
440
|
24 200
|
[60,70)
|
65
|
4
|
260
|
16 900
|
[70, 80)
|
75
|
2
|
150
|
11 250
|
42
|
1 820
|
88 050
|
Propiedades de la desviación típica
1. La desviación típica será siempre un valor
positivo o cero, en el caso de que las puntuaciones sean
iguales.
2. Si a todos los valores de la variable se les suma un número la desviación típica no varía.
3. Si todos los valores de la variable se multiplican por un número la desviación típica queda multiplicada por dicho número.
4. Si tenemos varias distribuciones con la
misma media y conocemos sus respectivas desviaciones
típicas se puede calcular la desviación
típica total.
Observaciones sobre la desviación típica
1. La desviación típica,
al igual que la media y la varianza, es un índice muy sensible a las
puntuaciones extremas.
2. En los casos que no se pueda hallar la media tampoco será posible hallar la desviación
típica.
3. Cuanta más pequeña sea la desviación
típica mayor será
la concentración de datos alrededor de la media.
MEDIDAS DE ASIMETRIA Y CURTOSIS
Las medidas de distribución nos permiten identificar la
forma en que se separan o aglomeran los valores de acuerdo a su representación
gráfica. Estas medidas describen la manera como los datos tienden a reunirse de
acuerdo con la frecuencia con que se hallen dentro de la información. Su
utilidad radica en la posibilidad de identificar las características de la
distribución sin necesidad de generar el gráfico. Sus principales medidas son
la Asimetría y la Curtosis.
1. ASIMETRÍA
Esta medida nos permite identificar si los datos se
distribuyen de forma uniforme alrededor del punto central (Media aritmética).
La asimetría presenta tres estados diferentes [Fig.5-1], cada uno de los cuales
define de forma concisa como están distribuidos los datos respecto al eje de
asimetría. Se dice que la asimetría
es positiva cuando la
mayoría de los datos se encuentran por encima del valor de la media aritmética,
la curva es Simétrica cuando se distribuyen aproximadamente
la misma cantidad de valores en ambos lados de la media y se conoce como asimetría negativa cuando la mayor cantidad de datos se
aglomeran en los valores menores que la media.
El Coeficiente
de asimetría, se representa mediante la ecuación matemática,
Ecuación 5-9
Donde (g1) representa el coeficiente de asimetría de Fisher,
(Xi) cada uno de los valores, ( )
la media de la muestra y (ni) la frecuencia de cada valor. Los resultados de
esta ecuación se interpretan:
)
la media de la muestra y (ni) la frecuencia de cada valor. Los resultados de
esta ecuación se interpretan:
·
(g1 = 0): Se acepta que la distribución
es Simétrica, es decir, existe aproximadamente la misma cantidad de valores a
los dos lados de la media. Este valor es difícil de conseguir por lo que se
tiende a tomar los valores que son cercanos ya sean positivos o negativos (±
0.5).
·
(g1 > 0): La curva es asimétricamente
positiva por lo que los valores se tienden a reunir más en la parte izquierda
que en la derecha de la media.
·
(g1 < 0): La curva es asimétricamente
negativa por lo que los valores se tienden a reunir más en la parte derecha de
la media.
Desde luego entre mayor sea el número (Positivo o Negativo),
mayor será la distancia que separa la aglomeración de los valores con respecto
a la media.
2. CURTOSIS
Esta medida determina el grado de concentración que
presentan los valores en la región central de la distribución. Por medio del Coeficiente de Curtosis, podemos
identificar si existe una gran concentración de valores (Leptocúrtica),
una concentración normal (Mesocúrtica) ó una baja concentración (Platicúrtica).
Para calcular el coeficiente de Curtosis se utiliza la
ecuación:
Ecuacion 5-10
Donde (g2) representa el coeficiente de Curtosis, (Xi) cada
uno de los valores, ( )
la media de la muestra y (ni) la frecuencia de cada valor. Los resultados de
esta fórmula se interpretan:
)
la media de la muestra y (ni) la frecuencia de cada valor. Los resultados de
esta fórmula se interpretan:
·
(g2 = 0) la distribución es
Mesocúrtica: Al
igual que en la asimetría es bastante difícil encontrar un coeficiente de
Curtosis de cero (0), por lo que se suelen aceptar los valores cercanos (± 0.5
aprox.).
·
(g2 > 0) la distribución es
Leptocúrtica
·
(g2 < 0) la distribución es
Platicúrtica
Cuando la distribución de los datos cuenta con un
coeficiente de asimetría (g1 = ±0.5) y un coeficiente de Curtosis de (g2 =
±0.5), se le denomina Curva Normal. Este criterio es de suma importancia ya que
para la mayoría de los procedimientos de la estadística de inferencia se
requiere que los datos se distribuyan normalmente.
La principal ventaja de la distribución normal radica en el
supuesto que el 95% de los valores se encuentra dentro de una distancia de dos
desviaciones estándar de la media aritmética (Fig.5-3); es decir, si tomamos la
media y le sumamos dos veces la desviación y después le restamos a la media dos
desviaciones, el 95% de los casos se encontraría dentro del rango que compongan
estos valores.
Desde luego, los conceptos vistos hasta aquí, son sólo una
pequeña introducción a las principales medidas de Estadística Descriptiva; es
de gran importancia que los lectores profundicen en estos temas ya que la
principal dificultad del paquete SPSS radica en el desconocimiento de los
conceptos estadísticos.
Las definiciones plasmadas en este capítulo han sido
extraídas de los libros Estadística
para administradores escrito
por Alan Wester de la editorial McGraw-Hill y el libro Estadística y
Muestreo escrito por Ciro Martínez editorial Ecoe editores (Octava edición).
No necesariamente tienes que guiarte por estos libros ya que en las librerías
encontraras una gran variedad de textos que pueden ser de bastante utilidad en
la introducción a esta ciencia.






















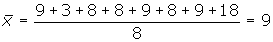








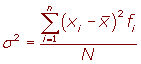


No hay comentarios:
Publicar un comentario